LOBSTgER

Disclaimer

This is not intended to be an academic publication, just an interesting read. For supporting documentation and related work, please refer to peer-reviewd publications. This is a collaborative work between Andreas P. Mentzelopoulos and Keith Ellenbogen. Generated images are subject to copyright by Andreas P. Mentzelopoulos and Keith Ellenbogen.

Summary

We attempt to address the challenge of obtaining high-quality underwater image data through generative modelling, specifically leveraging denoising-diffusion probabilistic models. The scarcity of high-quality underwater images poses significant obstacles to training underwater vision algorithms and in general is hindering progress in marine research and conservation efforts. Our work aims to bridge this gap by leveraging generative modeling techniques to produce realistic high-resolution underwater seascapes. We leverage a U-Net type architecture to train a latent diffusion model which learns to generate high-resolution (one dimension in the order of thousand pixels) underwater images of Jellyfish. Proof of concept is done on ImageNet and then the model is trained on images provided by Keith Ellenbogen.

Introduction

Diffusion models have swiftly become pivotal in modern image synthesis methodologies. Notably, they serve as the foundation for most of the widely adopted image generative models, like OpenAI’s DALL-E and Sora, demonstrating their effectiveness in producing diverse and high-quality images. Similar to Generative Adversarial Networks (GANs) and Variational Autoencoders (VAEs), diffusion models are designed to generate new images that closely adhere to the distribution of the training data.

The application of diffusion models in environmental imaging, particularly in underwater photography, remains relatively unexplored. However, the potential impact of such techniques is substantial. By generating high-fidelity images of underwater landscapes, diffusion models can facilitate research in marine biology, environmental conservation, and habitat monitoring. Furthermore, the ability to synthesize realistic images of marine ecosystems holds promise for educational outreach and public awareness campaigns aimed at promoting conservation efforts. In this work, we embark on a novel exploration by applying techniques from the field of diffusion models to create captivating seascapes featuring jellyfish.

Our objective is twofold: firstly, we aim to develop a denoising diffusion model. This model operates directly within the image space, taking original images as input and producing outputs that align with the characteristics of the training data. Secondly, we delve into latent space diffusion modeling to address scalability challenges. This approach involves integrating an autoencoder framework. Here, the encoder component transforms original images into latent representations, which are then fed into the diffusion model. Through iterative training, the model learns to generate new samples within the latent space, subsequently decoded back into image form via the decoder. This innovative method builds upon the work of Rombach et al. 2022 (“High-Resolution Image Synthesis with Latent Diffusion Models”), whose diffusion model architecture is based on the transformer framework.

By leveraging these advanced techniques, we aim to advance the field of image synthesis, particularly in the realm of underwater photography. Our endeavor holds promise not only for generating visually aesthetic representations but also for enhancing our understanding and appreciation of marine ecosystems, particularly those inhabited by jellyfish.

Related Work

While diffusion models share common objectives with other generative models such as GANs and VAEs, they offer distinct advantages in terms of training stability and sample quality. GANs, characterized by their adversarial training framework, often encounter challenges such as mode collapse and training instability. VAEs, on the other hand, prioritize the generation of images that closely match the distribution of the training data but may struggle with producing sharp and coherent samples. Diffusion models offer a compelling alternative by leveraging the iterative denoising processes to generate high-quality images while maintaining training stability. Recent advancements in diffusion modeling have led to variants of diffusion models which generate diverse and high-fidelity images from even textual descriptions.

Furthermore, the applicability of diffusion modeling extends beyond traditional image generation tasks to encompass a wide array of applications, including image denoising, super-resolution, and inpainting. For instance, denoising diffusion probabilistic models have demonstrated remarkable efficacy in image restoration, effectively removing noise while preserving crucial image details. Similarly, diffusion models have shown promise in medical imaging applications, contributing to denoising MRI images and enhancing diagnostic accuracy.

In the pursuit of high-resolution image synthesis, recent studies have explored novel approaches leveraging diffusion models. Stable diffusion and transformer-based architectures have built on the latent-diffusion framework and are capable of generating images with dimensions in the thousands of pixels.These advancements underscore the potential of diffusion models in pushing the boundaries of image synthesis, particularly in generating high-resolution images with unprecedented fidelity.

Data in Brief

We leverage access to two primary datasets that will serve as the foundation for training and evaluating our diffusion model. The first dataset, sourced from ImageNet, comprises of a few hundred images of jellyfish captured across diverse environmental conditions and perspectives. These images provide a rich and varied source of data, enabling us to train our preliminary diffusion model on a comprehensive range of jellyfish species, habitats, and lighting conditions. Some representative samples are displayed in the figure above.

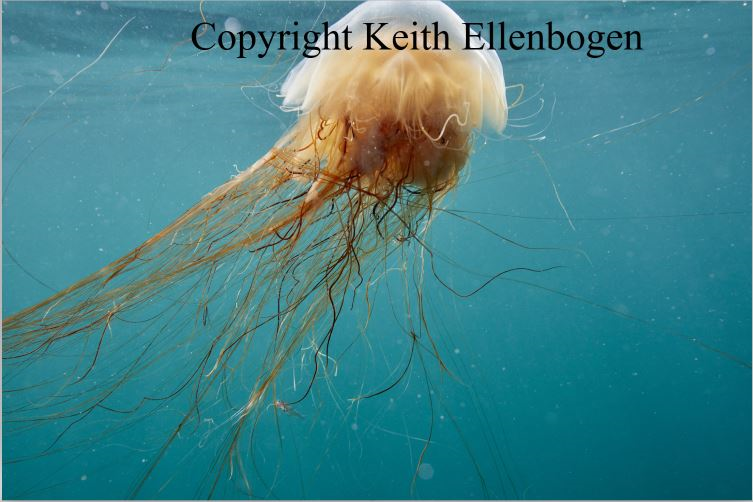
In addition we will leverage a supplementary dataset consisting of images by Keith Ellenbogen, Professor of photography at SUNY, specializing in marine life photography. Professor Ellenbogen’s images offer a unique perspective on jellyfish, characterized by their exceptional clarity, composition, and artistic merit. By incorporating those images into our training and evaluation pipeline, we aim to enhance the robustness and generalization capabilities of our diffusion model, ensuring its efficacy across a wide range of real-world scenarios and image styles. The data provided by Professor Ellenbogen constitute of 667 images of Lions Maine Jellyfish photographed within New England.

Together, these datasets provide a diverse and comprehensive foundation for our research, enabling us to develop and validate a diffusion model capable of generating high-quality seascapes featuring jellyfish with fidelity and realism. Through meticulous data curation, preprocessing, and augmentation, we ensure that our model learns to capture the intricate details and nuances inherent in jellyfish imagery, ultimately advancing our understanding and appreciation of these captivating marine creatures.

Denoising-Diffusion Probabilistic Models

Diffusion models are trained to generate image samples that faithfully adhere to the distribution of the data shown during training. In this study we employ the diffusion model proposed by Ho et al., 2020 (“Denoising Diffusion Probabilistic Models”). At the core of this model lies the concept of simulating the diffusion of noise throughout an image. This process unfolds in two main phases: the forward process and the reverse process. In the forward process, noise is gradually added to an initial image, creating a noise-corrupted version. This step mimics the diffusion of noise, progressively obscuring the original content of the image and transforming it into a Gaussian latent. Subsequently, in the reverse process, the model learns to ‘undo’ this diffusion, i.e. gradually removing the noise to reconstruct the original image. Through iterative refinement, the model hones its ability to accurately reverse the diffusion process, ultimately yielding high-quality reconstructions. Sampling a random Gaussian latent and reversing the diffusion allows one to generate new samples adhering to the distribution of the training samples.

Forward Diffusion

Starting from a data point (image) \(\mathbf{x}_0\), we can add noise using a Markov chain of \(T\) steps. At each step of the chain \(t\), we add Gaussian noise with variance \(\beta_{t}\) to \(\mathbf{x}_{t-1}\). This process is shown in Figure below (right). Assuming that the initial distribution of \(\mathbf{x}_0\) is \(q(x)\), the distribution of \(\mathbf{x}_{t}\) will be \(q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\), formulated as:

Defining \(a_t = 1 - \beta_t\) and \(\bar{\alpha}_t=\prod_{s=0}^t \alpha_s\), with \(\boldsymbol{\epsilon}_0, \ldots, \boldsymbol{\epsilon}_{t-2}, \boldsymbol{\epsilon}_{t-1} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\), then

so samples across all time steps may be efficiently computed in a single vectorized operation.

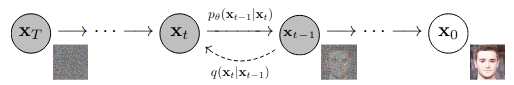
Reverse Diffusion

During reverse diffusion, a model learns \(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\), which is achieved by training a parameterized model \(p_{\theta}\) as shown above. Given \(p_{\theta}\) is Gaussian and parameterizing its mean and variance, we get:

In practice, the sample \(\mathbf{x}_0\) is re-parameterized as \(\mathbf{x}_0=\frac{1}{\sqrt{\bar{\alpha}_t}}\left(\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}\right)\) and a neural network is employed to approximate \(\boldsymbol{\epsilon}\), and, consequently, the mean \(\tilde{\boldsymbol{\mu}}_t\left(\mathbf{x}_t\right)=\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}\right)\). The loss function used for training usually is the MSE loss calculation between \(\tilde{\boldsymbol{\mu}}_t\left(\mathbf{x}_t\right)\) and \(\tilde{\boldsymbol{\mu}}_\theta\left(\mathbf{x}_t, t\right)\).

Latent Diffusion

Given that diffusion models were initially proposed to operate directly on an input image space, scaling the image resolution inevitably scales the amount of compute and memory required to learn the diffusion process. For high-resolution images, operating directly on the image space can thus become computationally prohibitive.

To mitigate this issue, latent diffusion models learn the diffusion process on embeddings of the original input image space. Usually the embeddings are low-dimensional representations of the input images obtained from autoencoders or variational-autoencoders. The diffusion process is then performed in the latent space of the autoencoder and data in the image space are obtained using the decoder.

Architecture and Training

In this study we develop a latent diffusion model enabling us to perform high-resolution image synthesis. Diffusion is performed on the latent space of a well studied autoencoder. The autoencoder model is a vector-quantized GAN proposed by Rombach et al., 2022 (“High Resolution Image synthesis with latend diffusion models”). The autoencoder used accepts images of dimensions (C, H, W) and transforms them into latents of (4, H/8, W/8). In our case, given input images of shape 3x640x1024, the latent representations were of size 4x80x128.

A U-Net type architecture was employed to learn the diffusion process in the latent space of the autoencoder. We employed the architecture proposed by Karras et al., 2023 (“Analyzing and Improving the Training Dynamics of Diffusion Models”). The model is comprised of encoder and a decoder blocks, which downsample and upsample the input respectively. The input to the U-Net is first passed through an embeddings block which transforms the input into embeddings which are distributed throughout the network to be further processed by the net. We employ 3 encoder blocks consisting of convolutional, normalization, and attention layers, with residual connections. Three (3) decoder blocks follow consisting of deconvolution, convolution, and attention layers with residual connections. Skip connections are leveraged to communicate information directly between the encoder and decoder blocks.

Regarding diffusion parameters, a set linear variance schedule was used with values ranging in (0.0001, 0.02). The number of diffusion steps was selected to be $ T = 1000$. The AdamW algorithm was used to optimize the model parameters with an initial learning rate of 1e-4 and a cosine annealing step scheduler. The U-Net was trained for 10k epochs on a V100 GPU.

Results

In this section we present the images we have been able to generate and attempt to quantify the results.

Diffusion on Image Space

Our first attempt was learning the diffusion directly on the image space. We used downsampled 64x64 images from either ImageNet or Keith Ellenbogen. We illustrate the reverse diffusion in the figure below. On the top left we illustrate the sampled Gaussian noise and show how the model gradually removes the noise to obtain a generated sample. Albeit the output is severely downsampled and the characteristics of the jellyfish are hard to distinguish, this approach served as a proof of concept for our diffusion model.

Latent Diffusion on Imagenet 256 x 256

Our second attempt was performing latent diffusion leveraging the autoencoder and data from ImageNet downsampled to a 256x256 resolution. The figure below illustrates the results. In this case, the results cannot be easily distinguished from the original samples that were used to train the model (indicative samples shown in Data in Brief section above). Thus, we can be confident that the model adheres to the initial data distribution. At this point we note that our model is able to generate images with the same resolution as Ho et al. (2020) with less compute required.

High Resolution Image Synthesis

Our final attempt was to train a latent diffusion model on images from Keith Ellenbogen at a resolution of 640x1024 pixels. We illustrate the results below. In the figure we show six samples of generated images which demonstrate the image variety of and clarity we are able to generate. We note that a Jv. Haddock can be spotted in some of the images as the training set included multiple pictures of the young Haddock seeking safety within the Jellyfish’s tentacles.

Conclusions

In this work, both a diffusion model and a latent diffusion model were implemented in order to generate medium-low (256\(^2\) — 64\(^2\)) and high resolution (640x1024) images of Jellyfish. The proposed framework was applied to data from ImageNet and data collected off the coast of New England provided by underwater photographer Keith Ellenbogen.

Although our framework can learn the diffusion process directly on the image space, employing a latent diffusion approach is significantly more efficient, enabling high resolution image synthesis while reducing the necessary compute. Using our framework, we are able to generate samples qualitatively similar to the training data while at the same time maintaining detail, clarity, realism, and sample diversity.